This is an old story, but a coworker and I were just discussing “The Monty Hall Problem,” which comes down to the common scenario from the old game show “Let’s Make a Deal”: If you have three doors, with a car behind one of them, and dud prizes behind the other two, once you’ve made your selection and the host reveals a dud prize behind one of the other doors, does it make sense for you to switch doors or stick with the one you’ve picked?
The simple intuitive answer is that it makes no difference, now that there’s a 50/50 shot at opening the right door. But it seems that 2/3 of the time it’s better to switch! We pondered this for a while and I guessed that it may have something to do with the fact that the host knows which door the car is really behind.
Apparently that’s correct. (Since this link points to an ancient [in Internet time] web page that may or may not endure, although it’s made it this long, I’ll provide a summary here.)
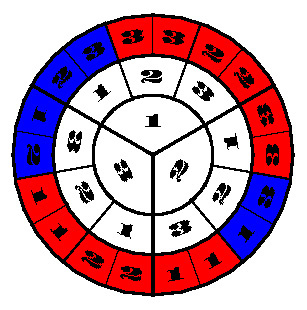
This roulette wheel is the key. The inner circle is the door the car is behind, the middle circle is the door the contestant picks, and the outer circle is the door(s) Monty Hall can open after the contestant picks. The red spaces indicate that the contestant should switch, and the blue that they should not. 2/3 of the time it’s better to switch, because Monty Hall has basically been forced to reveal that the car is behind the door the contestant did not pick.
In other words, the contestant picks the right door the first time 1/3 of the time. This is pretty straightforward. That means that 2/3 of the time they did not pick the right door the first time, also straightforward. Therefore, since 2/3 of the time the car is not behind the door they picked, and Monty Hall will never open the door the car is behind, then 2/3 of the time the car is behind the door that neither the contestant nor Monty Hall picked, so the contestant doubles their chance of winning by switching.