One of my web clients emailed me about a rash of fake orders they received a few days ago.
Usually these fake orders are for very small amounts, because the people (or bots) placing them are testing stolen credit cards, so they try to fly under the radar.
I’m not sure what was going on here. Needless to say, my client was unable to fulfill this order. And I’m not masking their IP address (the only part of this that isn’t fake) because they don’t deserve anonymity.
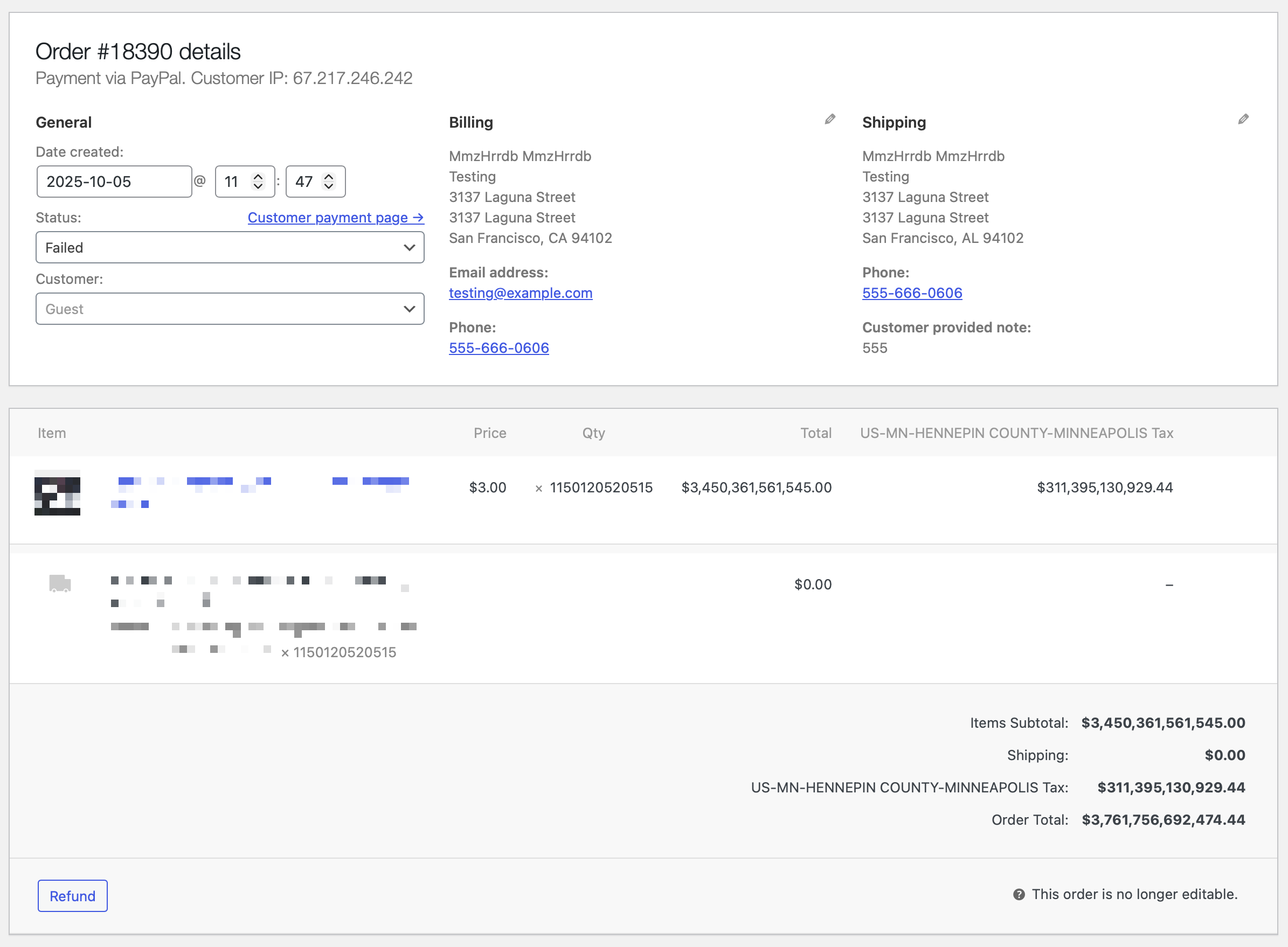
This person (most likely not a bot in this case) placed 174 orders in a span of just under 2 hours. Many of them were for reasonable amounts. Some were… like this. A few included clumsy attempts at code injection. None of them went through, of course, and no real harm was done. I’m just a bit mystified at what this person was hoping to achieve.
It almost seems like the work of a bored teenager, trying to flex their ersatz hacking skills.
It’s just kind of unfortunate that this wasn’t real. The sales tax alone could have fully funded the Minnesota and Hennepin County governments for quite a while. (I looked it up. The state’s revenue is around $2 billion per month. At that rate, this single order could have kept the state fully funded for about 13 years. Oh, and this was only one of several orders for amounts like this.)
It gets even better! I checked the order notes, and it turns out PayPal rejected the order because the quantity exceeded the allowed value. No shit. Why doesn’t WooCommerce limit the quantity input field? Ridiculous.
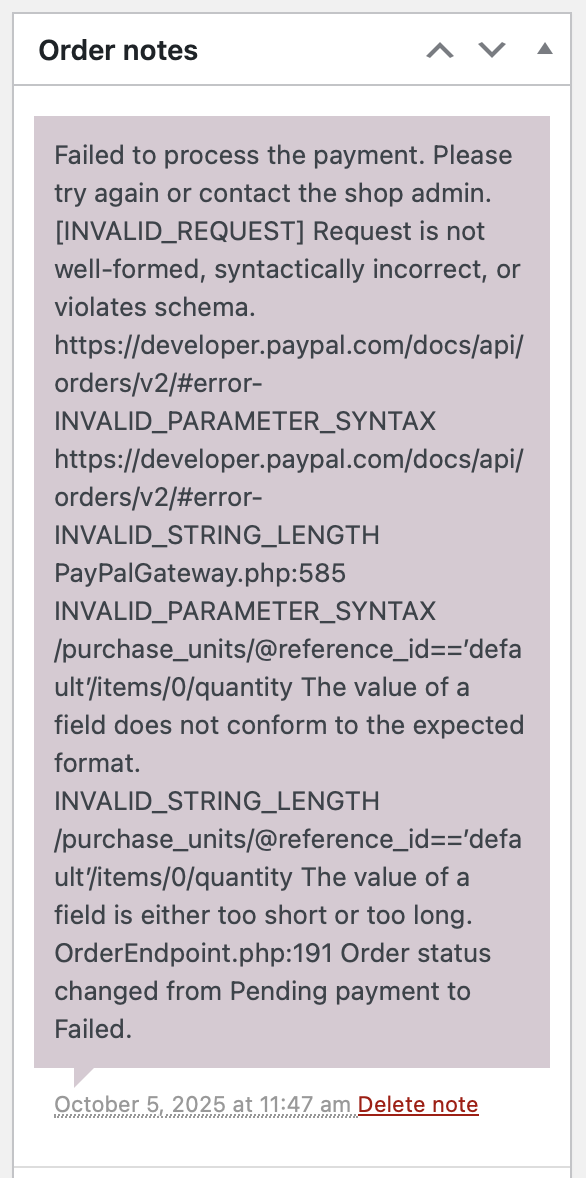
OK, so how do we fix this?
It seems obvious that we should be able to set a maximum value for the quantity input. And there are WooCommerce add-ons that give you a lot of flexibility to set minimum and maximum quantities on an individual product basis. There are plenty of reasons a complex ecommerce store might want or need those kinds of rules, but I want something more basic. I just want to set a hard upper limit of 100 on the quantity field for all products in this store.
The WooCommerce quantity field is an <input type="number"> field. And that field has min and max attributes you can use to set the valid number range. A number input is a special text input field that has up and down arrow keys that let you increment/decrement the value by amounts controlled by the step attribute.
But here is what I find absolutely fucking maddening about number inputs: you can also type in them. You can type whatever you want in them. You can type letters. Special characters. And worst, numbers outside the range dictated by the min and max attributes. Browsers are “supposed” to validate the input and prevent submitting the form, but in practice I’ve seen that both be extremely hit-or-miss, and also vary wildly from browser to browser.
It makes no sense to me at all why browsers allow anything other than numerical characters in a number input, i.e. the digits 0-9, plus periods, commas, and hyphens. Why? WHY???
Sometimes I really hate this job.
Anyway… let’s pretend number inputs don’t suck. Hooks make it easy to set the max value for the WooCommerce quantity input. Here’s what I used:
function my_woocommerce_quantity_input_args($args, $product) {
$args['max_value'] = 100;
return $args;
}
add_filter(
'woocommerce_quantity_input_args',
'my_woocommerce_quantity_input_args',
PHP_INT_MAX - 1, 2
);You could add a conditional to only set the max_value to 100 when it’s not already set (the default value is -1 by the way), although I was having some trouble getting that to work and I didn’t want to bother troubleshooting it any further… especially since, as indicated by my previous rant, max doesn’t actually do anything to prevent users from typing in a ludicrously large number, or the entire text of the Declaration of Independence, if they so desire. (OK, to be fair, in my testing, Safari’s validation does prevent you from submitting the form with text in the field. But it totally ignores the max value. And I don’t understand why it doesn’t just wipe out invalid characters as you type.)
Side note on my code snippet above: I like to ensure that my code isn’t going to get changed by something else that runs later, so I have a habit of setting the priority on WordPress hooks to PHP_INT_MAX - 1 to get it to run as late as possible. (I use the - 1 to give myself an “out” if I need to add something even later.)
Anyway… we still need a solution, and that’s where we have to resort to JavaScript. (Specifically I’m using jQuery because it’s WordPress.) It’s 2025 and we still have to use JavaScript to work around mind-numbingly basic limitations of HTML. ¯\_(ツ)_/¯
Here’s the jQuery code I wrote to both a) force the quantity input to only accept non-negative integers, and b) actually force the min and max limits, as the user types. (Of course someone could still get around this by disabling JavaScript, but I’m pretty sure there are other steps in the ordering process that would fail without it anyway.)
jQuery('input[type="number"].qty').on('change keyup', function() {
var min = jQuery(this).attr('min');
var max = jQuery(this).attr('max');
var q = jQuery(this).val();
q = q.replace(/\D/g, '');
if (typeof min != 'undefined' && min != '') {
if (Number(q) < Number(min)) { q = ''; }
}
if (typeof max != 'undefined' && max != '') {
if (Number(q) > Number(max)) { q = ''; }
}
jQuery(this).val(q);
});A few notes on this:
- I’m using
input[type="number"].qtyas the jQuery selector because it efficiently identifies the quantity input on both the individual product page and the cart page in WooCommerce. I also probably don’t need to watch both thechangeandkeyupevents but I wanted to cover all the bases. - After some trial and error with confusing behavior, I determined that the best UX for this comes from casting the values as
Number()right at the point of comparison, and changing the value not to theminormaxvalue, but to just empty it out. - The
.replace()method here uses a regular expression that rejects all non-numeric characters. If you need to accept negative numbers or fractions, you’ll need to change/\D/gto/[^\d.-]/gor/[^\d,-]/gif your locale uses commas as the decimal delimiter… or just/[^\d.,-]/gif you want to cover all the bases (and/or allow thousands separators). - Still I am finding some odd behavior here with
.replace()that I have never experienced before, and I’m having trouble narrowing down why. It seems to me that this code should be simply stripping non-numeric characters out of the string. So for example if I typed “56g” the value forqwould become56. But what I’m observing is that if the initial value forqis composed entirely of digits, it passes it along, but if there are any non-numeric characters in the string, the entire value gets wiped out. (I tested this with various regular expressions, e.g.\D,[^\d],[^0-9]etc. And I usedalert()to output the value ofqimmediately after the.replace()line, to make sure it wasn’t an issue with the subsequent logic. I am absolutely mystified by this, but I’ve already spent more time on it than I can bill to the client, so I need to stop here.) - I’ve been working with JavaScript for over 20 years, but it’s never been my primary area of emphasis… it still kind of feels like a foreign language to me, whereas PHP is my native tongue. So I don’t always do my JavaScript in the most “JavaScript-y” way.

